プログラミング演習(Advanced-1):最小2乗法
- 実験データの解析などに使われる、最小2乗法による近似式を求めるプログラムの作成です。
(理論)
n組のデータ (xi,yi) (i=1,2,...n) について一次関数
f(x)=ax+b ...........................
(1)
で近似することを考える。
データ yi と近似式 f(x) の偏差の二乗和 S
S=Σ[yi-f(x)]2 = Σ(yi-b-axi)2
................................
(2)
を最小にするように関数を近似する事を最小2乗法という。
この S を最小にする a, b を求めるには、a, b を変化させた時の S の極値、つまり S を a, b
で偏微分した量が0になる a, b の値、を求めれば良い。
∂S/∂a=-2 Σxi (yi -b -a xi)=0
∂S/∂b=-2 Σ(yi -b -a xi )=0
これより、a と b が
b=(Y S2 - X S1)/(S2 - X2)
................................ (3)
a=(S1 - X Y)/(S2 - X2)
................................ (3')
と表される。ただし、
S1=1/n Σ xi yi ,
S2=1/n Σ xi2, X=1/n Σ xi
,
Y=1/n Σ yi
である。
(課題P1−1)
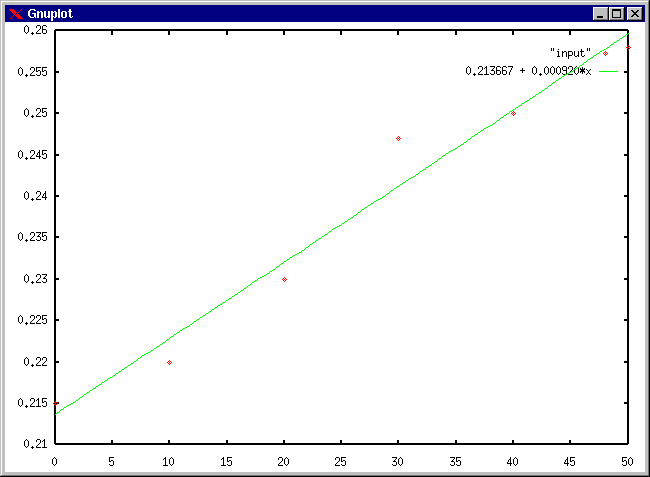
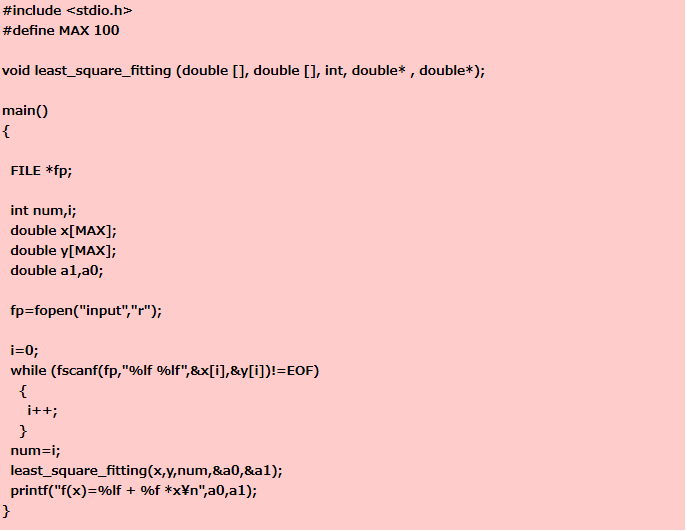
以下のプログラムは input
からデータを読み込み、そのデータについて最小2乗法によって直線近似を行うプログラムのメイン関数である。 関数
least_squre_fitting を作成し、プログラムを完成させなさい。
(注)
while (fscanf(fp,"%lf %lf",&x[i],&y[i])!=EOF)
の EOF (End Of File) はファイルの終りを意味する。つまりこの while
は、ファイルの先頭からデータを読んで行き、ファイルの終りが来るまでループを行う。

input
(右クリック、名前を付けてリンク先を保存、input として実行ファイルのあるディレクトリに保存)
式(2)の偏差の2乗和の平均値 S/N および 平方根の平均値 (√S)/N
を計算して出力するようにプログラムを変更せよ。どちらの値が誤差として妥当であるか吟味せよ。
(課題P1−3)
続いて最小2乗法について、直線の代わりに指数型関数
f(x)=a exp(bx)
で近似することを考えよう。上式の両辺のlog をとると
log(f(x))=log(a)+bx
となるから、A=log(a) とおけば、
F(x)=log(f(x)) =A+bx
という直線近似に変換できて、あとは課題1と同じ理論が使える。最小2乗法による指数型関数近似のプログラムを作成し
ましょう。
以下のデータ(1つ目のデータで確認する。もう1つのデータでも実行する)に適用しましょう。
gnuplot でプロットしてみること。
【1目のデータ】
x y
100 0.0005
150 0.0025
200 0.022
250 1.5
300 10.0
350 125.0
400 1280.0
gnuplot> plot "input2
gnuplot> replot exp(-13.421768 + 0.052408 *x)
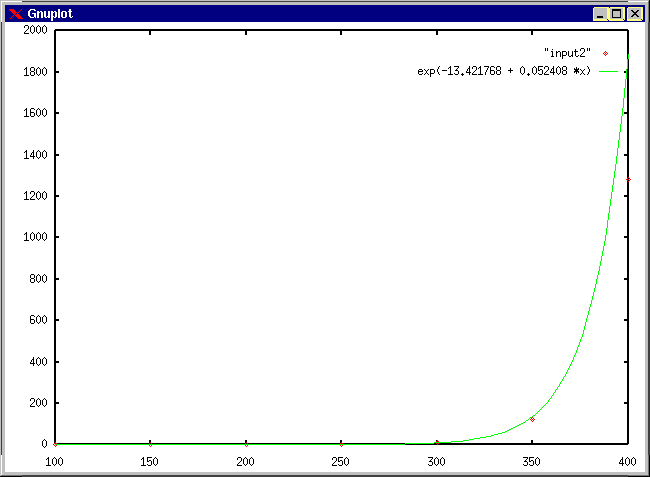
gnuplot> set log y
gnuplot> replot
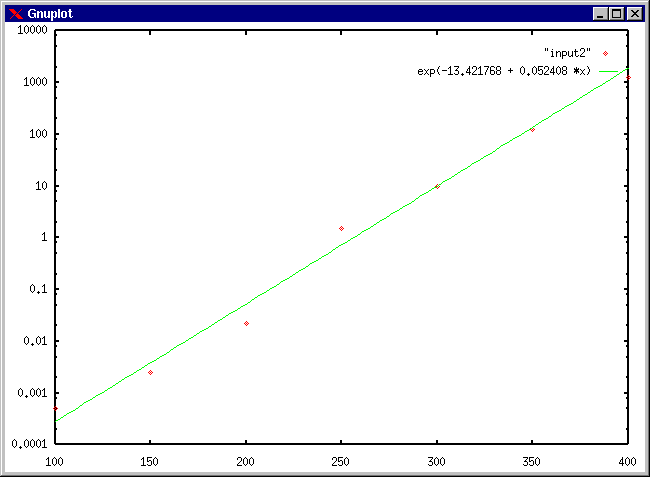
【2つ目のデータ】
x y
10 12.5
15 10.3
20 2.85
25 1.13
30 0.387
35 0.194
40 0.027
余裕のある人へ
(課題P1−4)
式 (3)と(3') を導出しなさい。また、前問で log
を取った時の誤差の評価をどうすべきか考察しなさい。
Shimpei Endo, The University of Electro-Communications