プログラミング演習（P1）：乱数とその応用

• 乱数とその応用
コンピュータの乱数は、予測できない現象の数値実験やコンピュータゲームなど、とても広い分野で使用されています。
 
• 関数 rand ()

関数 rand () は 0 から RAND_MAX までの整数の値の一様乱数を発生させる関数です。RAND_MAX  は機種によって異なります。rand() を使って[0,1)  (0 以上 1 未満) の乱数を発生させるには、以下のように関数 rand() からの値を  RAND_MAX  +1 で割ります。
 

#include <stdio.h>   #include <stdlib.h>  void main ()  {    double x;    for (i=0;i<=100;i++)      {        x=(double) rand()/ ((double)(RAND_MAX)+1.0);        fprintf(fp,"%d  %f\n",i,x);      }  .......  }

このプログラムでは x に次々に乱数が代入されていきます。
(double) は 変数を double 型に変更する演算子で、上のプログラムでは、(整数)／(整数)を実数で計算するために使われています。
 
•  乱数の性質(１)

数列が一様乱数であるかを確かめる方法の一つに度数分布による方法があります。乱数の区間を等分割し、各々の区間に入っている数列の要素数を数えます。

(例題P１−１)
下のプログラムは [0,1) の乱数の度数分布を調べるプログラムである。区間は２等分である。作成し、実行してみましょう。




（実行結果）
% ./a.out
 seed ? 2
 n ? 1000
0  <= x <0.5  : 469
0.5<= x <1    : 531

srand は乱数の種を設定する関数で引数には正の整数を代入します。

（課題P１−１）
上のプログラムで seed を変えて実行しなさい。結果がどうなるか観察しなさい。どのくらいのばらつきがあるか。平均値は？標準偏差は？プログラムを作ってもよいし電卓で計算してもよいです。


• ランダム・ウォーク
  

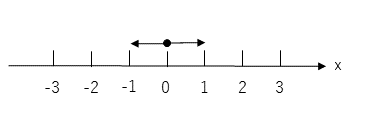
ランダム・ウォークとは、１次元の場合、

１）粒子は、１ステップごとに直線上を＋１または−１だけ移動する。
２）＋１か−１に進むのはそれぞれ２分の１の確率である。




という模型である。この模型はブラウン運動や気体分子の拡散などの物理学のいろいろな問題に応用されている。

(例題P１−２）以下のプログラムは、１次元のランダム・ウォークの計算を行うプログラムで、

• out.d というファイルを作成
• 乱数を生成
  
• i 番目の位置 ix を out.d に出力する

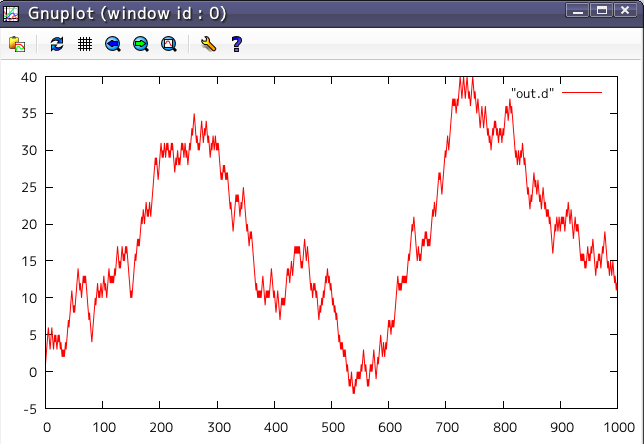
を行います。作成して実行し、横軸 i 縦軸 ix として gnuplot でプロットしましょう。



% gcc pex1-2.c -o pex1-2
% ./pex1-2
 seed ? 100
 n ? 1000

% gnuplot
gnuplot>plot "out.d" w l




(課題P１−２）
例題P1-2のプログラムを作成して、乱数の種 seed を変えて、グラフがどのようになるか観察してみよう。




---

ランダム・ウォークが、N ステップで平均してどのくらいの距離を進むかを考えてみよう。N ステップ経った時の位置を x_N とすれば、この地点の原点(始めの位置)からの距離の２乗 d_N は

d_N= x_N * x_N

である。d_N は始めの乱数の種にも依存する。そこで d_N の"平均値"が N に対してどのように依存するのか考えよう。ステップ数 N のとき、いろいろな乱数の種から始めて d_N の計算を M  回行い、それらを d_N(1), d_N(2), ...., d_N(M) とする。それらを使って 進んだ距離の平均値を　d_Nの平均値の平方根（√） をとったもの

√<d_N>= √ [ ( d_N(1)+d_N(2)+ ... + d_N(M) )/M ]

とする。

(課題P１−３）
ステップ数 N=100、初期値の数 M=10 として、距離の平均値  √<d_N> を計算しなさい。さらに、N=10000、 M=10として  √<d_N> を計算しなさい。計算には電卓を使ってもよいし、プログラムを作成してもよい。



---


M が大きくなると  √<d_N> がどの値に近づくか調べよう。例題のプログラムと電卓で計算するのはたいへんなので、プログラムを改良するとよい。
もし同じ乱数の種から計算を始めるといつも同じ d_N が得られてしまう。"平均値" をとるためにはいろいろな乱数の種から始めて d_N を計算を行う。いろいろな乱数の種から始める一つの方法は、N ステップの計算を M 回連続して繰り返すことである。つまり 、1 回目の N ステップの計算の種はインプットから与えて、２回目以降はその前の計算の最後の乱数を種とすれば良い。
結局、N 回のステップのためのループと 、それをM 回繰り返すためのループの２重ループをつくる。N ステップの計算を繰り返すたびに、それまでに得られた d_N から平均値を計算し、出力する。

(課題P１ー４)
（例題P１−２）の i のループの外側にもう１つループを作って √<d_N> を M 回計算するプログラムを作成しなさい。N=100 として　M=10, 100, 1000, 10000 として実行し、√<d_N> が、大きい M に対してどの値に近づくか予想しなさい。また、 同様に N=10000,
M=10, 100, 1000, 10000 として実行し、√<d_N> が、大きい M に対してどの値に近づくか予想しなさい。

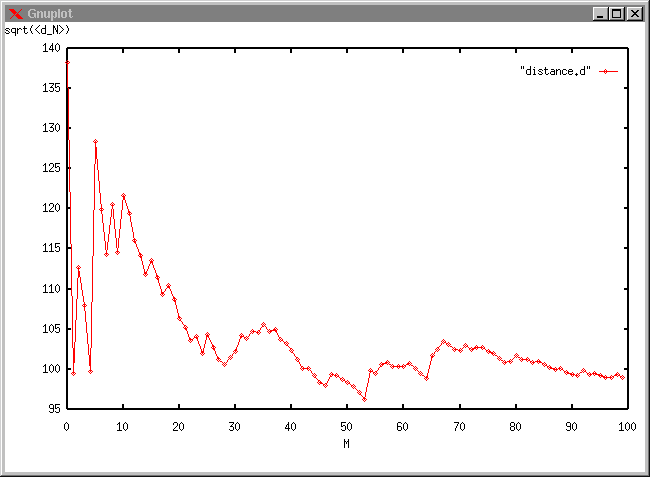
（参考）下の図は、N=10000 として、Ｍを変化させたときの √<d_N> の値を示したもの。




（余裕のある人へ）（課題P１−５）

２次元のランダム・ウォークで、課題P１−３と同様のことをやってみよう。２次元のランダム・ウォークの場合、


１、粒子は正方格子上を動く。
２、毎回でたらめな方向に動く。

という模型である。この模型はブラウン運動や気体分子の拡散などの物理学のいろいろな問題に応用されている。

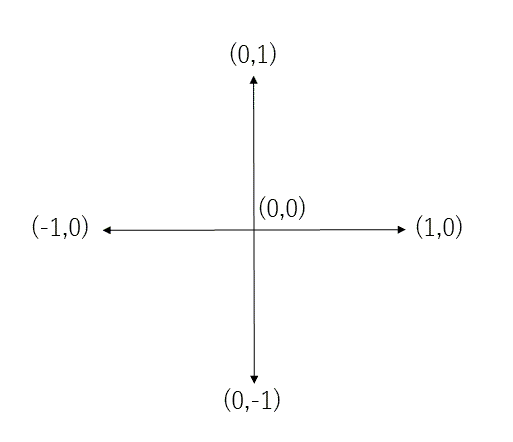
さて、２次元の場合、始めに (0,0) にある粒子は 、上下左右  (1,0), (-1,0), (-1,0), (1,0) のどれかに 1/4 の確率で動く。次に、動いた点からまた確率1/4 で上下左右に動く。これを N 回繰り返して、どこまで移動したかを調べる。








1. 粒子の X 座標、Y 座標の値 x, y を定義し(整数型)、x=0, y=0 に初期化する。
2. (課題１３−２)で使用した [0,1) の乱数プログラムを使って、出て来た値が
• [0,0.25) なら上へ (y の値を１だけ増やす)
• [0.25,0.5) なら下へ(yの値を１だけ減らす)
• [0.5,0.75) なら左へ(xの値を１だけ減らす)
• [0.75,01) なら右へ(xの値を１だけ増やす)
動く。
3. 動いた所の座標 x, y をファイルに出力する。
4. ２に戻る。
得られたデータを gnuplot でプロットし、観察せよ。乱数の種、ステップ数(繰り返しの数)を変えてみなさい。

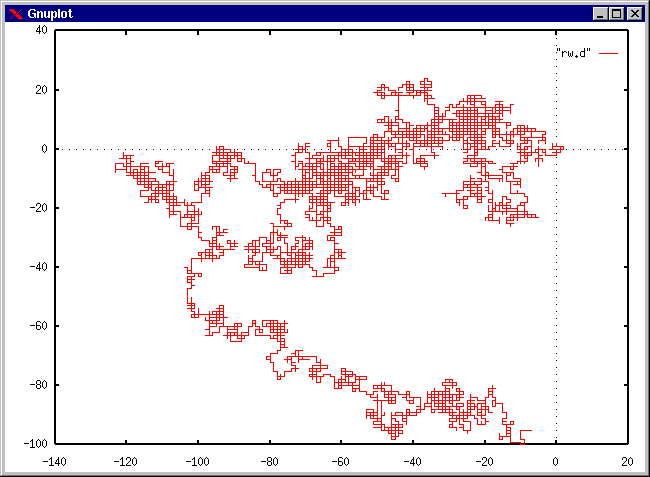
(例) 10000 ステップの例。gnuplot の "with line" は直線でデータを結ぶためのオプション。
% gnuplot
gnuplot> plot "rw.d" with line
gnuplot>





距離の平均を、


d_N= x_N * x_N + y_N * y_N

√<d_N>= √ [ ( dN(1)+dN(2)+ ... + dN(M) )/M ]

として、N=100, 10000 について、大きい M に対して　√<d_N> がどのように近づくか？


---

Shimpei Endo, The University of Electro-Communications