f(a)*f(b)<0 であったら x=[a,b] に解が存在する。a と b の中点を s として、f(a)*f(s)< 0 であったら [a,s] に解が存在するので b を s に置き換える。そうでなかったら [s,b] に解が存在するので a を s に置き換える。この操作を |a-b|< eps になるまで繰り返す。
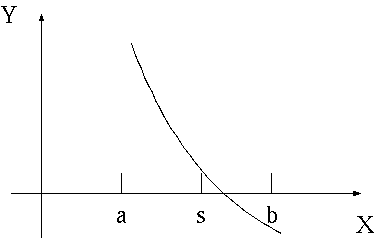
(例題P2−1)以下のプログラムは func で定義された関数 x3-3 = 0 を解いて 3 の3乗根を求めるプログラムである。作成して実行しなさい。

(実行結果)
gcc pex2-1.c -o pex2-1
./pex2-1
a=1.00000000000000 b=2.00000000000000 s=1.00000000000000
a=1.00000000000000 b=1.50000000000000 s=1.50000000000000
a=1.25000000000000 b=1.50000000000000 s=1.25000000000000
a=1.37500000000000 b=1.50000000000000 s=1.37500000000000
a=1.43750000000000 b=1.50000000000000 s=1.43750000000000
a=1.43750000000000 b=1.46875000000000 s=1.46875000000000
a=1.43750000000000 b=1.45312500000000 s=1.45312500000000
a=1.43750000000000 b=1.44531250000000 s=1.44531250000000
a=1.44140625000000 b=1.44531250000000 s=1.44140625000000
a=1.44140625000000 b=1.44335937500000 s=1.44335937500000
a=1.44140625000000 b=1.44238281250000 s=1.44238281250000
a=1.44189453125000 b=1.44238281250000 s=1.44189453125000
a=1.44213867187500 b=1.44238281250000 s=1.44213867187500
a=1.44213867187500 b=1.44226074218750 s=1.44226074218750
a=1.44219970703125 b=1.44226074218750 s=1.44219970703125
a=1.44223022460938 b=1.44226074218750 s=1.44223022460938
a=1.44224548339844 b=1.44226074218750 s=1.44224548339844
a=1.44224548339844 b=1.44225311279297 s=1.44225311279297
a=1.44224929809570 b=1.44225311279297 s=1.44224929809570
a=1.44224929809570 b=1.44225120544434 s=1.44225120544434
a=1.44224929809570 b=1.44225025177002 s=1.44225025177002
a=1.44224929809570 b=1.44224977493286 s=1.44224977493286
a=1.44224953651428 b=1.44224977493286 s=1.44224953651428
a=1.44224953651428 b=1.44224965572357 s=1.44224965572357
a=1.44224953651428 b=1.44224959611893 s=1.44224959611893
a=1.44224956631660 b=1.44224959611893 s=1.44224956631660
a=1.44224956631660 b=1.44224958121777 s=1.44224958121777
a=1.44224956631660 b=1.44224957376719 s=1.44224957376719
x=1.44224957376719
(課題P2−1)
上のプログラムを参考に 15 の5乗根を計算するプログラムを作成し実行しなさい。f(x) について関数を使う。
上の例では、 eps=1.e-8 とした。eps=1.e-10 として収束性を調べなさい。正しい値に近づいているか確かめなさい。
さらに 50 の5乗根を計算するようにしなさい。(25=32<50 に注意しなさい。初期条件。)
(課題P2−2)
a と b を入力し、xb -a = 0 を解いて a の b 乗根(または a の 1/b
乗)を求めるプログラムを作成せよ。ただし、b は正の整数としてよい。
関数 pow の値と比較できるようにしなさい。 いくつかの a と b で計算してみなさい。
初期値を x0 とし、y=f(x) と x0 で接する直線 y = f’(x0)
(x-x0) + f(x0) が 0 となる x を x1
とする。すなわち、
x1= x0 - f(x0)/f'(x1)
これを繰り返して、 n+1 回目では、
xn+1= xn - f(xn)/f'(xn)
となる。|xn+1 - xn| < eps となるまで繰り返す。
(例題P2−2)以下のプログラムは func で定義された関数 x3-3 = 0 を解いて 3 の3乗根を求めるプログラムである。作成して実行しなさい。
gcc pex2-2.c -o pex2-2
./pex2-2
x0, x=2.00000000000000 1.58333333333333
x0, x=1.58333333333333 1.45444752231456
x0, x=1.45444752231456 1.44235158435782
x0, x=1.44235158435782 1.44224957752245
x0, x=1.44224957752245 1.44224957030741
x=1.44224957030741
(課題P2−3)
上のプログラムを参考に 15 の5乗根を計算するプログラムを作成し実行しなさい。関数 func と dfunc を変える。
2分法と比べて繰り返しの回数はどうなっているか?
また、初期値 x0 を x0=10, 100, 1000 として繰り返し回数を調べなさい。なぜそうなるか?
(課題P2−4)
上のプログラムでは、関数 f と微分 f’に対して func と dfunc の2つの関数を使った。関数をまとめて f と f'
についての関数を1つだけ使うようにプログラムを変更しなさい。
(課題P2−5)
a, b, c, d を入力し、ax3 + bx2 + cx +d = 0
を解を求めるプログラムを作成せよ。P2-4 と同様に、f と f' の関数を1つだけ使う。a=6, b=-7, c=-3 として
x の値を求めよ。得られた値をもとの式に代入し、解になっていることを確かめなさい。実数解の個数などを吟味しなさ い。