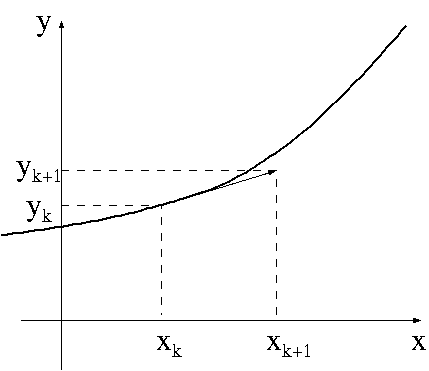プログラミング演習（P４）：常微分方程式

　　y'=f(x,y), x₀ ≦ x ≦ x_N
　　y(x₀)=y₀

の数値解法を考える． 分点 x₀ < x₁ < x₂ < ... <x_N-1< x_N　をとり，分点 x_kで の値を y_k とし，簡単のため分点は等間隔 h であるとする．ここでは，オイラー法とルンゲ・クッタ法を取り上げる．

• オイラー法

x_k での微分を

　　y'=(y_k+1-y_k)/h + O(h²)

と直線で近似すると，微分方程式は，

　　y_k+1=y_k+ h f(x_k,y_k）+ O(h²)

と表すことができる．この式に (x₀, y₀) を代入すると ｙ₁が 求まる．同 様に，(x₁, y₁) を代入すると ｙ₂が求ま る．このように次々代入して y_N が求まる．

上述のように微分方程式を解く方法をオイラー法という．オイラー法の１ステップの誤差（局所誤差）は２次であり，多ステップ計算した結 果は，誤差（大域誤 差）は h の１次であることが知られている．一般に局所誤差が m+1 次のとき大域誤差は m  次であり，このような近似を与える式を  m  次の近似式という．
 


 

 
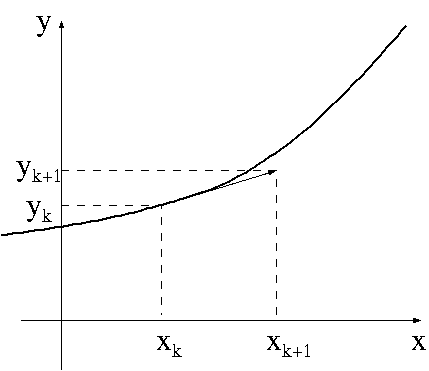
（例題P４−１）
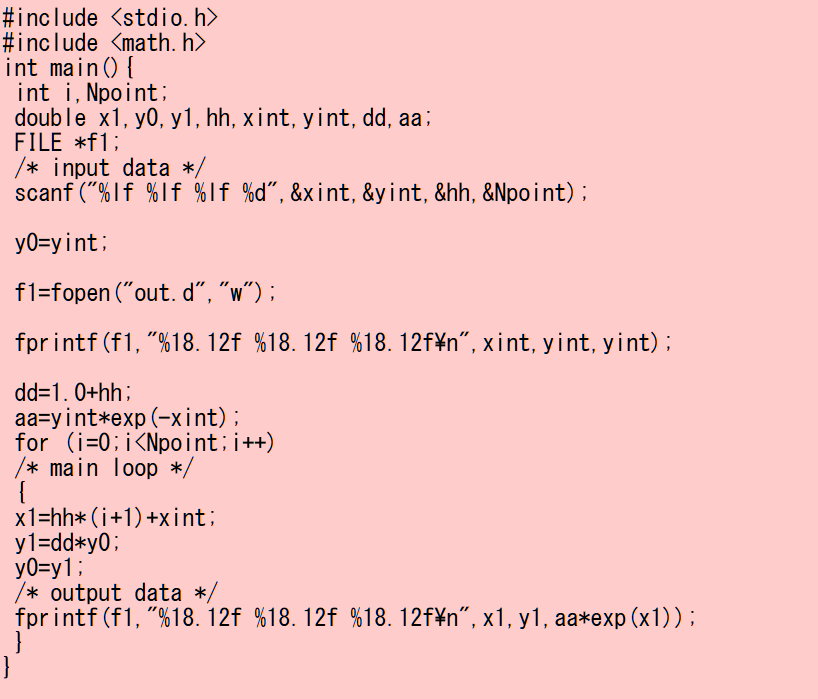
下のプログラ厶は微分方程式

dy/dx=y

を初期値 y(x₀)=y₀ として 一次の近似で解くプログラ厶です．x の分点は等間隔 h です．作成して実行してみましょう．
入力は、
（x の初期値）　（y　の初期値）　(分点の幅 h)  (繰り返しの数)
です。
プログラムでは、y1=y0+hh*y0 の代わりに dd=(1.0+hh) として y1=dd*y0 としてある。






出力結果をファイルに保存して，gnuplot で確認しましょう．
 
% gcc pex4-1.c -o pex4-1 -lm
% ./pex4-1
% 1 1 0.1 20
% gnuplot
gnuplot> plot "out.d", "out.d" using 1:3 w l


 


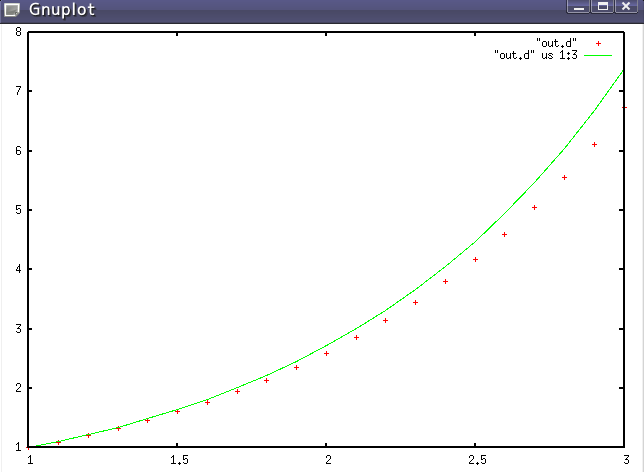
１行目は　x の値、２行目は y の値、３行目は解析解です。赤の点が計算値で、緑の線が解析解です。


---

（課題P４ー１）
上の例では分点の幅 h=0.1 とした。分点の幅を 1/10 つまり h=0.01 として計算しなさい。（繰り返しは１０倍にしなさい）計算値は解析解に近づくか確かめなさい。

（課題P４ー２）相対誤差＝｜（計算値ー解析解）/解析解｜を計算して、out.d の４行目に出力するようプログラムを変更しなさい。 h=0.1, 0.01, 0.01... として分点の幅を1/10　にすると、相対誤差はどうなるか、調べなさい。


（課題P４ー３）原子核は，ある有限の寿命で崩壊する．時刻 t での原子核の個数 N(t) の減少量，すなわち崩壊速度 -dN(t)/dt は，N(t)　に比例することが知られている．着目する原子核の個数が半分になる時間（半減期）T を適当な単位（例えば「年」）で入力して，N(t) についての微分方程式をオイラー法により求めるプログラムを作成せよ．適当な原子核 （例えば ¹⁴C，半減期 5.73 × 10³ 年）について計算実行せよ．解析解と比較せよ．きざみ幅 h を変えると結果どうなるか吟味せよ．

---



（課題P４ー４）
一定地域での生物集団を考える．単位時間の増殖率を a とすると，時刻 t での個体数 N(t) は
dN/dt=aN
と表される．ふつう，増殖率は一定ではなく，個体数が大きくなると（環境の悪化等で）減る傾向がある．増殖率が
a=c-bN (b,c は定数）
である場合のプログラ厶を作成せよ．解析解と比較せよ． t->∞ で解はどうなるか．c, b の物理的な意味を吟味せよ．

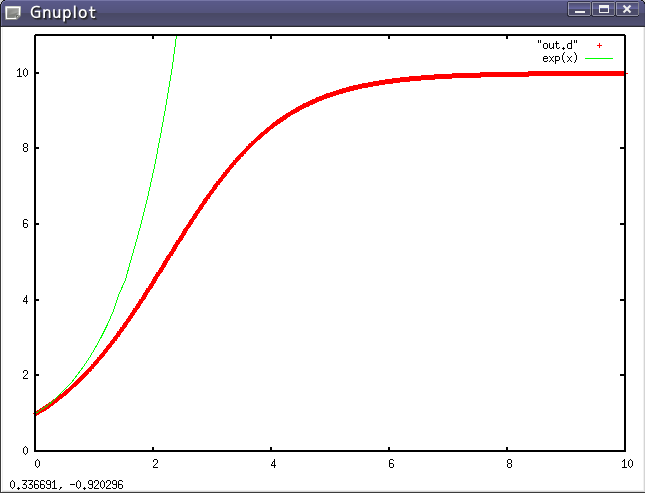
（結果の例)a=1, b=0.1の場合、初期値として x=1 で y=1 とした。赤の点が計算値、緑の線は b=0 の場合の解析解。

（余裕のある人へ）
（課題P４ー５）
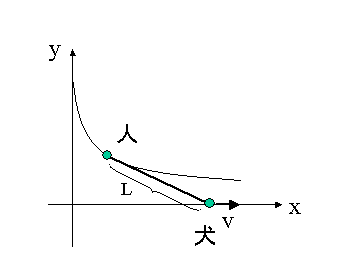
長さＬのひもの一端に犬をつないで他端を人が持っている．初めにひもがぴんと張った状態で静止していた．あるとき，犬が急に人を引きずって， ひもと垂直方 向に一定の速度で走り出した．この場合の人の運動の軌跡を求めたい． 時刻 0 での犬の位置を原点に、人の位置を (0,L) とし、犬は x 軸に沿って走るとする。人の速度はひもの方向を向いているので、人の位置 (x,y) は、
dy/dx= -y/sqrt(L²-y²)
で表される。これをオイラー法により計算せよ。時刻 0 で、dy/dx の値を十分大きい負の値、たとえば-10¹⁰ などとする。 また、解析解と比較せよ．

---

Shimpei Endo, The University of Electro-Communications