プログラミング演習（P５）：常微分方程式

　　y'=f(x,y), x₀ ≦ x ≦ x_N
　　y(x₀)=y₀

の数値解法を考える． 分点 x₀ < x₁ < x₂ < ... <x_N-1< x_N　をとり，分点 x_kで の値を y_k とし，簡単のため分点は等間隔 h であるとする．ここでは，オイラー法とルンゲ・クッタ法を取り上げる． 

---

• ルンゲ−クッタ法（２次）

オイラー法は 1 次の近似公式であった．近似の精度をあげる方法はいろいろあるが，ここでは応用上簡単な，以下の公式（２次のルンゲークッタ法 の１つ）を考えよう．

この式の局所誤差は３次であり，２次の近似公式である．
 

（例題P５-１）
下のプログラムは２次のルンゲークッタ法で y'=y の初期値問題を解くプログラムです。作成して実行してみましょう。





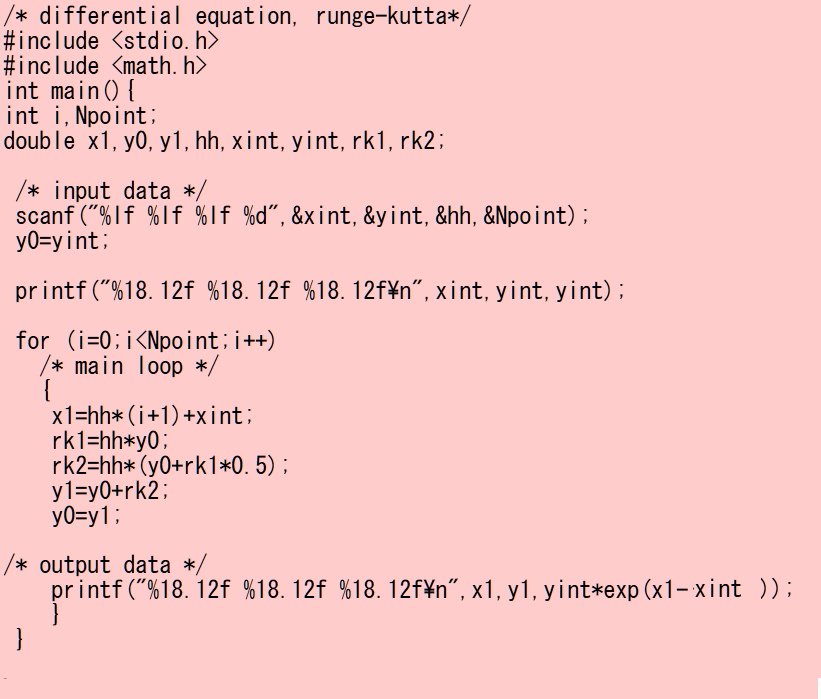
このプログラムでは、結果は画面に出力されます。出力結果を（リダイレクト > などを使って）ファイルに保存して，gnuplot で確認しましょう．


---

inp5 の中身 (前回のと同じ)
xの初期値、yの初期値、刻み幅、繰り返し

1 1 0.1 20

% gcc pex5-1.c -o pex5-1 -lm
%./pex5-1 <inp5 >out5
% less out5 <-- 中身の確認
% gnuplot <-- gnuplot で描画
 gnuplot> plot "out.d" <-- 前回の計算結果(オイラー法)をプロット
 gnuplot> replot "out5" <-- 今回の計算結果 (ルンゲ-クッタ法)をプロット
 gnuplot> replot "out5" us 1:3 w l   <-- 解析解をプロット



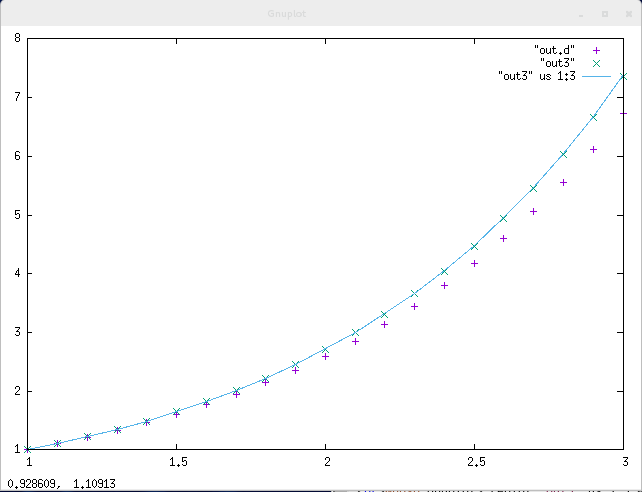
出力結果をファイルに保存して，gnuplot で確認しましょう．

---

（課題P５-1）
上のプログラムについて、相対誤差＝｜（計算値ー解析解）/解析解｜を計算して、結果と同時に出力するようプログラムを変更しなさい。 きざみ幅を変えて，収束性を調べなさい。 オイラー法の結果と比較分析しなさい。  


---

（課題P５-2）
空気中での物体に働く抵抗は速度の２乗に比例するという． 質量を m とすると、鉛直方向速度 v についての運動方程式は

m dv/dt=-mg+mkv²

と書ける。ただし、k の符号はv>0 （上向き）ならk<0、v<0 (下向き) なら k>0 である。 初期速度、質量、を与えて物体の時々刻々の速度 v を求めるプログラ厶を作成せよ． 手足を広げた人間について k=0.003 (1/m) であるとして、終端速度はいくらか。 終端速度の 9 割に達する時間はいくらか？

---

（課題P５-3）
抵抗 R（Ω），コイル L（H），電源E が直列につながったRC回路を考える．ある時刻 t での電流 I(t)は

L dI(t)/dt+RI(t)=E(t)


で表される．t=0 で電源のスイッチをいれて電圧を E(t)=Vsin(t) (t≧0) とした時の電流を計算する２次の Runge-Kutta のプログラ厶を作成しなさい．きざみ幅を変えて，収束性をしらべよ．
 

---

（余裕のある人へ）


（課題P５-4）
上のルンゲ−クッタ法の公式の局所誤差が３次であることを示せ．


---

Shimpei Endo, The University of Electro-Communications